Objectifs:
- Connaître le vocabulaire
- Savoir reconnaître et prendre et en considération les différentes sources d’erreurs lors d’une expérience :
- erreurs systématiques : erreurs de méthode, erreurs instrumentales, erreurs de manipulations…
- erreurs aléatoires : temps de réaction, modification des conditions expérimentales…
- erreurs grossières
- Savoir estimer l’incertitude absolue d’une mesure
- Savoir calculer l’incertitude relative d’une mesure
- Savoir calculer la valeur la plus probable et l’incertitude absolue d’un résultat en utilisant la valeur centrale entre les valeurs minimale et maximale
- Être capable de comparer un résultat expérimental et une valeur théorique ou de référence
- Savoir interpréter un résultat obtenu avec une calculatrice en tenant compte de la cohérence entre les mesures prises et les chiffres significatifs du résultat
- Savoir prendre des mesures et les mettre en correspondance dans un tableau de valeurs et dans un système d’axes avec rectangles d’incertitude
- Dans le cas de suites proportionnelles
- savoir calculer le facteur de proportionnalité (avec son incertitude)
- savoir calculer un élément manquant d’une des suites
Théorie:
livre p. 174 – 179
mais aussi
- La notion de mesure
Mesurer une grandeur consiste à comparer cette grandeur avec une grandeur de la même espèce, choisie comme unité. On obtient ainsi un nombre que l’on fait suivre du symbole de l’unité de la grandeur.
- Suite de mesures
Idéalement, en répétant un grand nombre de fois la mesure d’une même grandeur, dans des conditions rigoureusement identiques, on pourrait s’attendre à obtenir toujours le même résultat. En réalité, du fait de l’imperfection de nos sens et des instruments, on n’obtient pas un nombre unique, mais une de nombres, appelée suite de mesures.
Exemple: mesure du temps nécessaire pour 10 oscillations d’un pendule
| 10,12 | 10,15 | 10,08 | 10,21 | 10,15 |
| 10,21 | 10,09 | 10,08 | 10,06 | 10,09 |
| 10,14 | 10,02 | 10,07 | 10,13 | 10,13 |
| 10,13 | 10,16 | 10,12 | 10,14 | 10,20 |
| 10,02 | 10,14 | 10,17 | 10,10 | 10,18 |
| 10,12 | 10,12 | 10,25 | 10,00 | 10,04 |
La dispersion d’une suite de mesures est inévitable.
Le résultat de la mesure d’une grandeur n’est donc pas un nombre exact, mais un intervalle entre les limites duquel il est très probable que la vraie grandeur se situe.
- Valeur la plus probable
La valeur la plus probable d’une suite comportant un grand nombre de mesures est donnée par la moyenne arithmétique de tous les termes de la suite.
Pour la suite des 30 mesures du temps de 10 oscillations du pendule, cette valeur est égale à :

- Incertitude absolue
A partir d’une suite de mesures, il est possible de considérer un intervalle, centré sur la valeur la plus probable, entre les limites duquel se situe une partie importante de toutes les mesures (par exemple environ 70% de toutes les mesures).
Exemple: pour la suite des mesures ci-dessus, 22 mesures sont comprises dans un intervalle limité par 10,04 et 10,20. Dans ce cas 73,33% des 30 mesures que comporte cette suite appartiennent à cet intervalle.
L’écart entre les limites de cet intervalle et la valeur la plus probable est une bonne indication sur la dispersion de la suite. Cet écart représente l’incertitude absolue sur le résultat de la mesure.
On notera finalement, pour indiquer le résultat de la mesure du temps des 10 oscillations:
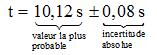
- Estimation de l’incertitude absolue
Lorsqu’il n’est pas possible de répéter un grand nombre de fois la mesure d’une même grandeur, on se contente d’estimer au mieux les limites de l’intervalle déterminant l’incertitude absolue.
- Si un instrument comporte une échelle graduée, on admet généralement que les mesures sont affectées d’une incertitude absolue égale à la valeur d’une demi-division de la graduation de l’instrument.
- Si l’instrument est digital, l’incertitude absolue correspond à la valeur d’une unité du dernier chiffre affiché.
- Incertitude relative sur une mesure
L’incertitude relative caractérise la précision d’une mesure. Une mesure est d’autant plus précise que son incertitude relative est faible.
L’incertitude relative est le rapport de l’incertitude absolue Ia(M) à la valeur la plus probable M. Elle se calcule donc comme suit:
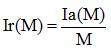
- Comment tenir compte des incertitudes dans un calcul
Lorsque les opérations que l’on est amené à effectuer sont des additions, des soustractions, des multiplications et des divisions, les règles suivantes peuvent être appliquées:
Somme de deux mesures:
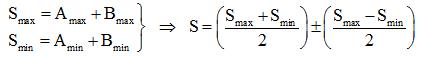
Différence de deux mesures:
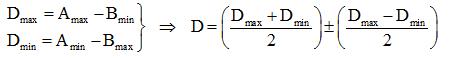
Produit de deux mesures:
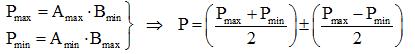
Quotient de deux mesures:
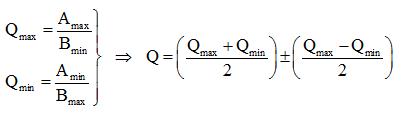
- Chiffres significatifs et incertitudes
D’une manière générale, on indique les incertitudes absolues avec un chiffre significatif. On arrondi ensuite la valeur approchée jusqu’à ce que l’incertitude absolue porte sur le dernier chiffre non arrondi.
Exemples :
Calcul du produit de A =10,12 ± 0,08 et de B = 8,2 ± 0,5
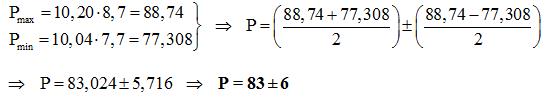
Calcul du quotient de A =10,12 ± 0,08 et de B = 8,2 ± 0,5
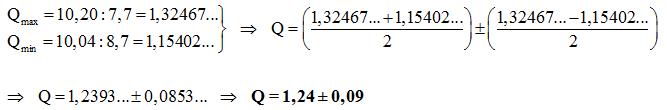
Exercices faits en classes:
mesure de la période d’oscillation d’un pendule (50 mesures -> courbe de résultats), MI01, 02, 03, 04, 05, 06, 07, 08, 09, 11, 13, 14, 15, 17, 18, 19, 26, 28, 29, 30, 32
Exercices distribués en classe:
Exercices supplémentaires (accès au corrigé en cliquant sur l’exercice) :
Prétest: