Objectifs :
- Développement de la vision dans l’espace, notamment par :
- la représentation de plans, de droites et de polyèdres en perspective cavalière
- le dénombrement des deltaèdres, des polyèdres réguliers (dits solides de Platon), avec justification
- le développement et la construction de divers polyèdres, notamment des polyèdres réguliers, semi-réguliers et tronqués
- la description de polyèdres et des duaux de polyèdres réguliers selon leurs propriétés : types de faces, etc. en utilisant la relation d’Euler
- le calcul de la longueur de l’arête, de l’aire, du volume ou d’une grandeur manquante d’un polyèdre, en utilisant le théorème de Pythagore ou le calcul algébrique
- la représentation d’un polyèdre selon les vues « de face », « de dessus » et « depuis la droite »
- la détermination de l’intersection d’un plan avec un autre plan, un cube, un prisme droit ou une pyramide
- Rédaction du compte rendu d’une recherche comprenant des démarches mathématiques en mettant en évidence les trois parties suivantes :
- Introduction : partie dans laquelle l’élève reformule la question, présente le problème et effectue si nécessaire une figure d’étude
- Recherche : partie dans laquelle l’élève présente sa démarche expérimentale contenant des calculs structurés ou des phases d’aller-retour entre question, hypothèse et expérience ; l’élève analyse ensuite sa démarche en menant une réflexion, en émettant des conjectures ou en justifiant un résultat obtenu
- Conclusion : partie dans laquelle l’élève rappelle les principaux résultats obtenus et répond à la question posée
Théorie :
Coup de pouce p 127 à 139
Le dual d’un polyèdre p est le polyèdre dont les sommets sont les centres de gravité des faces du polyèdre p.
Le centre de gravité d’un triangle est à l’intersection des trois médianes du triangle.
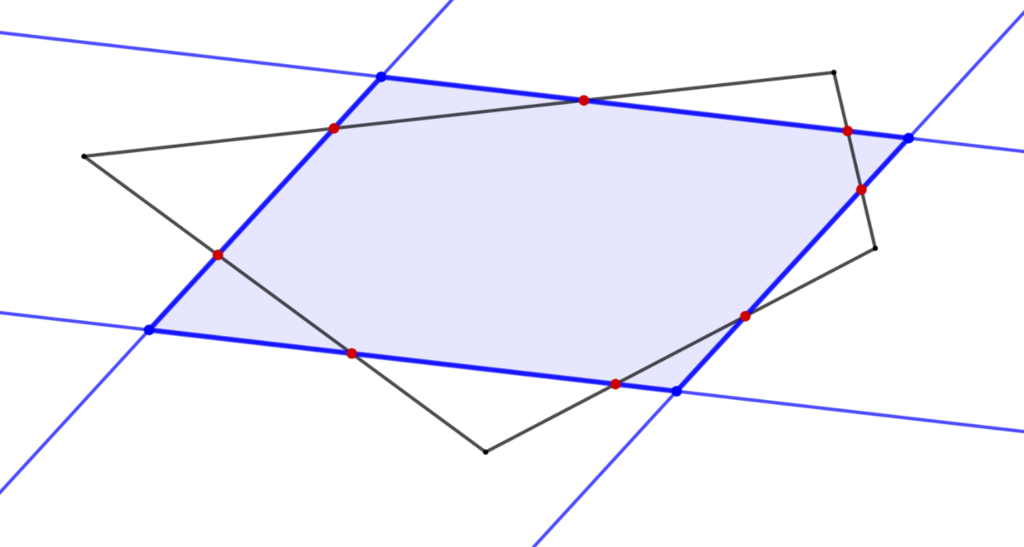
Pour un quadrilatère quelconque le théorème de Wittenbauer nous donne un manière de trouver le centre de gravité : « Dans le cas d’un quadrilatère non croisé, le centre de gravité du quadrilatère coïncide avec le centre du parallélogramme de Wittenbauer qui lui est associé ». Le parallélogramme de Wittenbauer étant le parallélogramme obtenu à partir du quadrilatère quelconque en découpant chaque côté de celui-ci en trois segments de même taille et en traçant les droites passant par deux points adjacents à un même sommet.
Exercices faits en classe :
PO 2, 4, 5, 8, 9, 18, 19, 20, 21, 22, 27, 36, 37, 38, 41, 42, 43, 44, 45, 48, 51, 54, 55, 56, 57, 59, 60, 61, 62, ex. suppl. projections orthogonales (série 1)
Exercices supplémentaires faits en classe :
Exercices supplémentaires :
- Projections orthogonales (3D -> 3 vues) : série 1, série 2, série 3, série 4, série 5, série 6
- Projections orthogonales (3 vues -> 3D) : série 1, série 2, série 3, série 4, série 5
- Intersection d’un plan et d’un cube : série 1, série 2, série 3
Test :