11H – VP – FA3 – Fonctions et diagrammes

Exemple d’application des fonctions quadratiques

La balistique est l’étude du mouvement d’un mobile qui a lieu sous l’effet de l’attraction terrestre au voisinage du sol. Tout frottement de l’air est négligé. Un tel mouvement se situe dans un plan vertical. On peut donc le décrire en tant que mouvement à deux dimensions. C’est encore Galilée qui, le premier, a donné une analyse correcte de ce mouvement.

Pour le mouvement balistique, la théorie aristotélicienne proposait une succession de mouvement distinct qui s’échelonnaient dans le temps. La trajectoire devait être tout d’abord rectiligne, s’arrondir ensuite en arc de cercle au passage du sommet, puis redescendre en mouvement rectiligne jusqu’au sol.

Galilée, abandonnant cette vue un peu naïve des choses, va poser les bases du mouvement balistique. Il imagine pour commencer qu’un corps roulant sur une table horizontale va, lorsqu’il arrive à son extrémité, continuer son mouvement horizontal (l’attraction terrestre agit verticalement, la composante horizontale de la vitesse n’est donc pas modifiée) tout en tombant simultanément dans un « mouvement naturel » (chute libre verticale).

La séparation du mouvement balistique en deux composantes indépendantes: un MRU (Mouvement Rectiligne Uniforme) horizontale et un MRUA (Mouvement Rectiligne Uniformément Accéléré) vertical, constitue une contribution capitale de Galilée à la compréhension de cette cinématique. Il montrera qu’une conséquence de cette séparation des mouvements est que les trajectoires balistiques sont des paraboles.

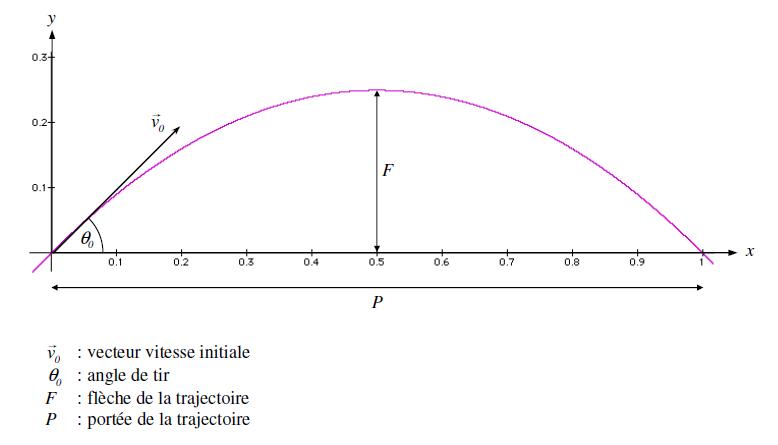
Dans cette situations les équations du mouvement sont:

En éliminant la variable t des deux équations précédentes, on exprime la trajectoire du projectile de la manière suivante :

Objectifs :

• Connaître le vocabulaire
• Savoir
  • reconnaître des situations pouvant être modélisées par des fonctions
  • lire et interpréter de tableaux de valeurs, de représentations graphiques
  • représenter une relation où interviennent deux grandeurs variables
    • par un tableau de valeurs
    • par une représentation graphique (à la main, à l’aide d’un tableur, d’un grapheur, …)
    • par une expression fonctionnelle (ou mathématique)
  • passer d’une représentation à une autre :
    • de l’expression fonctionnelle au tableau de valeurs et inversement
    • du tableau de valeurs à la représentation graphique et inversement
    • de l’expression fonctionnelle au tableau de valeurs et à la représentation graphique (fonctions constante, linéaire, affine, inverse, quadratique)
    • de la représentation graphique à l’expression fonctionnelle
  • résoudre des problèmes faisant intervenir des fonctions
  • interpréter et réaliser des diagrammes

Théorie :

Aide-mémoire pages 38 à 50

Tutoriels vidéo:

• représenter une fonction affine: vidéo 1, vidéo 2
• déterminer l’expression d’une fonction affine : vidéo 1, vidéo 2
• déterminer l’expression d’une fonction affine dont le graphique passe par deux points: vidéo 1
• étude de la fonction carrée: vidéo 1
• étude de la fonction inverse: vidéo 1
• déterminer l’extremum d’une fonction quadratique: vidéo 1
• déterminer les variations d’une fonction quadratique: vidéo 1
• étudier les variations de la fonction racine carrée: vidéo 1
• étudier les variations de la fonction cubique: vidéo 1

Animations GeoGebra:

• fonction affine : animation
• fonction quadratique: animation

Exercices faits en classe:

FA 3, 5, 6, 7, 129, ex. suppl. « images et antécédents » (S1), 8, 9, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20, 22, 24, 25, 26, 27, 29, 30, 32, 33, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, ex. suppl. « fonctions linéaires » (S1), 67, 68, ex. suppl. « fonctions affines » (S1), 54, 55, 60, 61, ex. suppl. « fonctions quadratiques » (S1), 56, 59, optimisation, 69, 70, 73, 74, 75, 79, 80, 81, 83, 86, 87, 91, 95, 96, 97, 98, 100, 103

FA 106, 107, 108, 109, 110, 111, 112, 114, 115, 116, 117, 118, 119

Exercices distribués en classes :

• images et antécédents: série 1 (+ corrigé)
• fonctions linéaires: série 1 (+ corrigé)
• fonctions affines: série 1 (+ corrigé)
• fonctions quadratiques: série 1
• optimisation: série 1 (+ corrigé)

Exercices d’entraînement:

• images et antécédents: série 1, série 2
• fonctions affines:
  • expression fonctionnelle si on connaît deux points de la droite : série 1
  • tracer le graphique en connaissant l’expression fonctionnelle: série 1, série 2
  • retrouver l’expression fonctionnelle à partir du graphique: série 1
  • divers: série 1, série 2, série 3
• fonctions quadratiques:
  • maximum ou minimum : série 1
  • associer une expression fonctionnelle à un graphique: série 1, série 2
• optimisation: série 1
• calculs de vitesses: série 1 (+ corrigé), série 2 (+ corrigé)

« Prétest »:

• TA 1 (fonctions constantes, linéaires et affines)
• TA 2 (fonctions constantes, linéaires et affines)
• TA 3 (fonctions constantes, linéaires, affines et quadratiques)
• test 1
• test 2 (fonctions constantes, linéaires et affines)
• test 3 (fonctions quadratiques et optimisation)
• test 4 (fonctions quadratiques + vitesse)