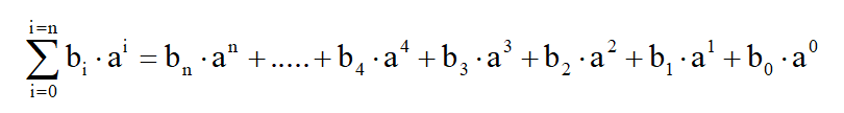Objectifs : x
- Connaître le vocabulaire
- Savoir
- analyser de différents systèmes de numération
- utiliser différentes bases de numération
- calculer dans les différentes bases de numération
- Savoir
- utiliser des clés et des fonctions pour coder et décoder un message
- utiliser la congruence pour résoudre des problèmes
Théorie :
La base est le nombre qui sert à définir un système de numération.
La base du système décimal est dix alors que celle du système octal est huit et celle du système binaire est 2.
Quelque soit la base numérique employée, elle suit la relation suivante :
où bi : chiffre de rang i
et ai : puissance de la base a d’exposant i
Exemples :
- En base 10 : 3412 = (3 x 103) + (4 x 102) + (1 x 101) + (2 x 100)
- En base 5 : 112 = (4 x 52) + (2 x 51) + (2 x 50) ⇒ (112)10 = (422)5
Système décimal
Le système décimal est celui dans lequel nous avons le plus l’habitude d’écrire.
Chaque chiffre peut avoir 10 valeurs différentes : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, de ce fait, le système décimal a pour base 10. Tout nombre écrit dans le système décimal vérifie la relation suivante :
745 = 7 × 100 + 4 × 10 + 5 × 1
745 = 7 × 10 × 10 + 4 × 10 + 5 × 1
745 = 7 × 102 + 4 × 101 + 5 × 100
Chaque chiffre du nombre est à multiplier par une puissance de 10 : c’est ce que l’on nomme le poids du chiffre.
L’exposant de cette puissance est nul pour le chiffre situé le plus à droite et s’accroît d’une unité pour chaque passage à un chiffre vers la gauche.
12 435 = 1 × 104 + 2 × 103 + 4 × 102 + 3 × 101 + 5 × 100 .
Cette façon d’écrire les nombres est appelée système de numération de position.
Dans notre système conventionnel, nous utilisons les puissances de 10 pour pondérer la valeur des chiffres selon leur position, cependant il est possible d’imaginer d’autres systèmes de nombres ayant comme base un nombre entier différent.
Système octal
Le système octal utilise un système de numération ayant comme base 8 (octal ⇒ latin octo = huit). Il faut noter que dans ce système nous n’aurons plus 10 symboles mais 8 seulement : 0, 1, 2, 3, 4, 5, 6, 7. Ainsi, un nombre exprimé en base 8 pourra se présenter de la manière suivante : (745)8
Lorsque l’on écrit un nombre, il faudra bien préciser la base dans laquelle on l’exprime pour lever les éventuelles indéterminations (745 existe aussi en base 10).
Ainsi le nombre sera mis entre parenthèses (745 dans notre exemple) et indicé d’un nombre représentant sa base (8 est mis en indice).
Cette base obéira aux même règles que la base 10, vue précédemment, ainsi on peut décomposer (745)8 de la façon suivante :
(745)8 = 7 × 82 + 4 × 81 + 5 × 80
(745)8 = 7 × 64 + 4 × 8 + 5 × 1
(745)8 = 448 + 32 + 5
Nous venons de voir que :
(745)8 = (485)10.
Système binaire
Dans le système binaire , chaque chiffre peut avoir 2 valeurs différentes : 0, 1.
De ce fait, le système a pour base 2. Tout nombre écrit dans ce système vérifie la relation suivante :
(10 110)2 = 1 × 24 + 0 × 23 + 1 × 22 + 1 × 21 + 0 × 20
(10 110)2 = 1 × 16 + 0 × 8 + 1 × 4 + 1 × 2 + 0 × 1
donc : (10110)2 = (22)10 .
Système héxadécimal
Le système hexadécimal utilise les 16 symboles suivant : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. De ce fait, le système a pour base 16. Un nombre exprimé en base 16 pourra se présenter de la manière suivante : (5AF)16
Le nombre (5AF)16 peut se décomposer comme suit : (5AF)16 = 5 × 162 + A × 161 + F × 160
En remplaçant A et F par leur équivalent en base 10, on obtient :
(5AF)16 = 5 × 162 + 10 × 161 + 15 × 160
(5AF)16 = 5 × 256 + 10 × 16 + 15 × 1
donc = (5AF)16 = (1455)10
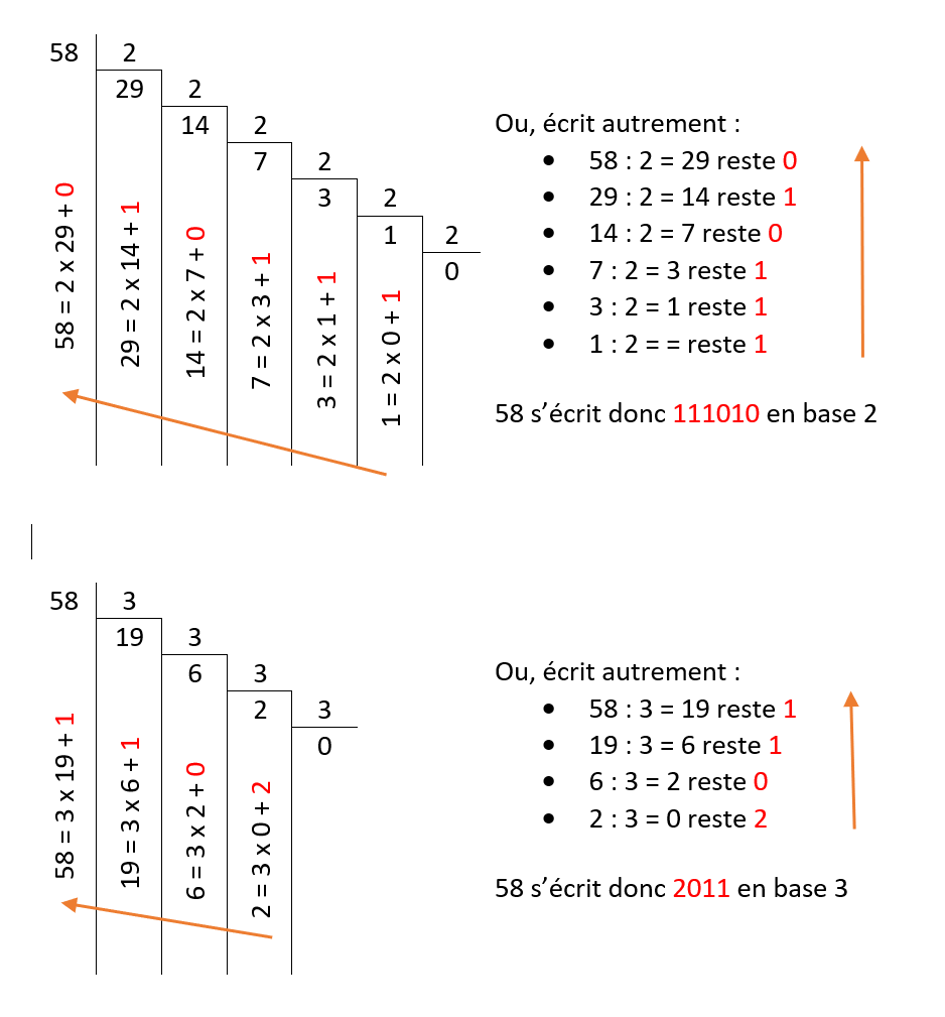
La division comme moyen de conversion de la base 10 dans une autre base :
Pour convertir un nombre donné en base 10 dans une autre base (2 à 9), on peut procéder par divisions successives en gardant les restes. Voici deux exemples :
« Applications » pour effectuer des changements de bases
Codes secrets
voici quelques fichiers Excel permettant de coder :
- codeur par décalage (code de Jules César)
- codeur par phrase clé
vidéo intéressante pour comprendre la notion de congruence.
Exercices faits en classe :
- CO 68, 70, 71, 74
- CO 87, 88, 89, 92, 96a,b, 98, 99, 100, 101
- CO 105, 106, 109, 110, 111, 113, 114, 115, 117, 118, 120, 121, 122, 123, 124, 125, 126
Exercices supplémentaires :
Tests :