Objectifs:
- Connaître le vocabulaire
- Comprendre la notion de mesure du temps notamment par :
- l’expérimentation du fonctionnement de systèmes de mesures
- la mise en relation de la mesure du temps et de phénomènes astronomiques (calendriers)
- Savoir
- calculer de proportionnalité et des échelles
- utiliser la notation scientifique
- transformer des unités entre mètre [m], unité astronomique [ua] et année(s)-lumière
- transformer des unités de temps (h, min, s) et d’angles (°, ‘, »)
- Comprendre et connaître le Système International d’unités (SI) et transformations d’unités en unités du SI : kilogramme, mètre et seconde
Système international d’unités (SI):
Faire une mesure, c’est comparer une grandeur physique (ou chimique) inconnue avec une grandeur de même nature prise comme référence à l’aide d’un instrument.
Qui dit mesure, dit référentiel, donc unité. Dans un passé pas si lointain, coexistaient de nombreuses unités qui n’avaient souvent que peu de rapports les unes avec les autres. Il a fallu attendre la révolution française pour qu’un premier système d’unités cohérent voit le jour : le système métrique. Ce système fût consacré sur le plan international par la Convention du mètre du 20 mai 1875, traité diplomatique.
En 1960, lors de la onzième Conférence générale des poids et mesures (CGPM), apparaît le Système International d’unités, le SI, qui comprend aujourd’hui deux classes d’unités :
- les unités de base, au nombre de sept ;
- les unités dérivées.
Cependant, il ne faudrait pas croire que ce système, une fois établi, reste figé. Les progrès de la science et des technologies, les nouveaux besoins de la société, et par conséquence les nouveaux besoins en terme d’exactitude accrue, amènent le LNE et l’ensemble des instituts nationaux de métrologie à améliorer, de façon constante et continue, la réalisation pratique de l’ensemble des unités du SI. Cette préoccupation concerne aussi bien les références que les moyens de transfert vers les utilisateurs, pour permettre de répondre au mieux à ces nouveaux besoins. Il est donc parfois nécessaire de faire évoluer les définitions des unités ou d’en introduire de nouvelles.
A ce jour, le Système International d’unités, le SI, est constitué de sept unités de base (entre parenthèse le symbole qui la représente de façon unique) :
- le mètre (m) (vidéo)
- le kilogramme (kg) (vidéo)
- la seconde (s) (vidéo)
- l’ampère (A) (vidéo)
- le kelvin (K) (vidéo)
- la candela (cd) (vidéo)
- la mole (mol) (vidéo)
| mètre (m) | Le mètre est la longueur du trajet parcouru dans le vide par la lumière pendant une durée de 1/299 792 458 de seconde. |
| kilogramme (kg) | Le kilogramme est la masse du prototype en platine iridié qui a été sanctionné par la Conférence générale des poids et mesures tenue à Paris en 1889 et qui est déposé au Bureau International des Poids et Mesures. |
| seconde (s) | La seconde est la durée de 9 192 631 770 périodes de la radiation correspondant à la transition entre les deux niveaux hyperfins de l’état fondamental de l’atome de césium 133. |
| ampère (A) | L’ampère est l’intensité d’un courant électrique constant qui, maintenu dans deux conducteurs parallèles, rectilignes, de longueur infinie, de section circulaire négligeable et placés à une distance de un mètre l’un de l’autre dans le vide, produirait entre ces conducteurs une force de 2 x 10-7 newton par mètre de longueur. |
| kelvin (K) | Le kelvin est la fraction 1/273,16 de la température thermodynamique du point triple de l’eau. |
| candela (cd) | La candela est l’intensité lumineuse, dans une direction donnée, d’une source qui émet un rayonnement monochromatique de fréquence 540 x 1012 hertz et dont l’intensité énergétique dans cette direction est 1/683 watt par stéradian. |
| mole (mol) | La mole est la quantité de matière d’un système contenant autant d’entités élémentaires qu’il y a d’atomes dans 0,012 kilogramme de carbone 12. |
Les unités dérivées sont nombreuses et viennent compléter les unités de base. Elles peuvent avoir des noms spéciaux (hertz, pascal, becquerel, …) mais peuvent toujours être exprimées à partir des unités de base. Il existe aussi des unités dérivées sans dimension.
Il est aussi à noter que ces unités sont reliées entre elles pour former un système cohérent.
Enfin, chaque grandeur peut avoir à couvrir une vaste étendue de valeurs. Pour éviter d’avoir à utiliser des facteurs multiplicatifs ou des valeurs avec un grand nombre de zéros, on a recourt à des préfixes. Ces derniers vont permettre de couvrir une gamme allant de 1024 à 10-24 fois l’unité.
Changements d’unités de longueurs :

Changements d’unités de masses :


Changements d’unités de temps:
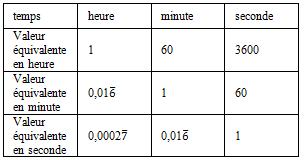
Exemples:
- transformer un code séxagésimal de temps en un code décimal de temps :
- 2 h 24 min 36 s = 2 + (24:60) + (36 : 3600) =2 + 0,4 + 0,01 = 2,41 h
- 12 h 48 min 45 s = 12 + (48 : 60) + (45 : 3600) = 12 + 0,8 + 0,0125 = 12,8125 h
- transformer un code décimal de temps en un code séxagésimal de temps :
- 7,605 h :
- 7,605 – 7 = 0,605
- 0,605 x 60 = 36,3 (transformation en minutes)
- 36,3 – 36 = 0,3
- 0,3 x 60 = 18 (transformation en secondes)
- 7,605 h = 7 h 36 min 18 s
- 7,605 h :
Exercices fait en classes :
- AS 16, 01, 02, 03, 04, 05, 11, 12, 13, 18, 19, 20
Vidéos :
- « C’est pas Sorcier » : les calendriers
- « C’est pas Sorcier » : mètre-kilogramme-seconde
Exercices distribués en classe:
temps:
- date de début et de fin : série 1, série 2
- temps écoulé entre deux heures: série 1
- changements d’unités de temps : série 1
Exercices supplémentaires:
temps:
- date de début et de fin : série 1, série 2
- temps écoulé entre deux heures: série 1, série 2
- changements d’unités de temps : série 1, série 2
arrondis : série 1, série 2, série 3
écriture scientifique : série 1, série 2
Prétest: